Learning-to-augment in Deep Learning

Chest X-ray images are used in deep convolutional neural networks for the detection of COVID-19, the greatest human challenge of the 21st century. Robustness to noise and improvement of generalization are the major challenges in designing these networks. In this paper, we introduce a strategy for data augmentation using the determination of the type and value of noise density to improve the robustness and generalization of deep CNNs for COVID19 detection. Firstly, we present a learning-to-augment approach that generates new noisy variants of the original image data with optimized noise density. We apply a Bayesian optimization technique to control and choose the optimal noise type and its parameters. Secondly, we propose a novel data augmentation strategy, based on denoised X-ray images, that uses the distance between denoised and original pixels to generate new data. We develop an autoencoder model to create new data using denoised images corrupted by the Gaussian and impulse noise. A database of chest X-ray images, containing COVID-19 positive, healthy, and non-COVID pneumonia cases, is used to fine-tune the pre-trained networks (AlexNet, ShuffleNet, ResNet18, and GoogleNet).

Learning-to-augment Strategy

Data Augmentation with Noisy Images: Adding noise to data is one approach to data augmentation. We present a method for learning-to-augment via noisy input images. The learning-to-augment finds optimal noise parameters to generate the new data. The mean and variance are parameters of the Gaussian and speckle noise types. The impulse (salt-and-pepper) noise is, on the other hand, specified with density parameter. The parameters of different noise models are: \(\mu\): the mean of Gaussian and speckle noise, \(𝑣\): the variance of Gaussian and speckle noise, and \(d\): the noise density of impulse noise. As shown in Fig 1, the proposed noisy image-based augmenter is composed of a noisy data generator, a controller, an augmenter, and child models. The steps of the noise-based data augmentation strategy are following:

• Step 1: Noisy data generator adds noise to the original images with specific noise parameters. In the first iteration, the parameters of noise are set randomly. Then, the controller determines the parameters of each noise type as a new policy.
• Step 2: The augmenter produces new data by applying the noise to the images.
• Step 3: The child CNN models are trained using new augmented data to evaluate the performance of data augmentation policies.
• Step 4: The controller, a Bayesian optimizer-based search algorithm, substitutes existing weak policies with new data augmentation policies by exploring the search space of the parameters for each noise type.
• Step 5: The above steps are repeated until the best policies, i.e., the parameters of each noise type, are found.

As shown in Fig. 1, to augment the data, the input data pool is first divided into \(N\) equal folds. Then a noisy data generator adds noise (e.g., impulse, Gaussian, speckle, and Poisson noise) to each fold separately. The raw samples of the dataset were randomly split into \(N\)-folds to accelerate finding the best policies. Decreasing the number of samples using the \(N\)-fold split reduces the CNN training time for each fold.

The augmenters create new data based on new parameters that the Bayesian optimizer has found. In the next step, each fold is processed by the child CNN model. Use of child networks, instead of very deep CNN, in policy evaluation speeds up the execution of the proposed method. Based on the results of child CNNs, the controller improves weak policies and maintains strong policies. The controller uses the Bayesian optimizer to find the optimum set of augmentation policies (the parameters of each noise type) in a search space. Let \(g\) be the search space and \(f\) be the loss function of a classifier, then the Bayesian optimizer can be represented as:

The optimization problem in above equation aims to find \(y\) that minimizes \(f(G)\) for \(G\) in a bounded domain \(g\). The loss values of the child CNNs are used to calculate the loss function for the Bayesian optimizer. This process continues until the maximum iteration number is reached.

Data Augmentation Approach with Denoised Data: The proposed method provides an automatic augmentation policy search method using the generation of restored images that had been corrupted by noise. Noisy images can be restored by enhancement algorithms such as autoencoder networks. However, depending on the noise type and density, the pixel values in the restored image and the original noise-free image are not exactly equal. We aim to leverage the dissimilarity between restored and original pixels as a data augmentation strategy. First, noise of specific type and density is added to the image. Then, the noise is partially removed from the image by using the proposed autoencoder. The denoising autoencoder aims to produce the output from the noisy input, where the target is set as the original images. Finally, the restored images are used as augmented data. In the proposed noise-based data augmentation algorithm, the type and density of noise are important. Depending on the accuracy of the noise removal algorithm, the restored image could be very similar to the original image, especially when the noise magnitude is low, which could thus result in an ineffective augmented image. On the other hand, if the noise magnitude is high and the denoising is imperfect (as expected), the pixel values of the restored images would be more dissimilar from the original ones. As shown in Fig. 2, noise parameters is added to the original images by the noise generator. The noisy samples are then fed as inputs to the proposed autoencoder Select \(N\) types of noise based on data type Randomly split raw samples of dataset to \(N\)-folds.

Data

We accumulated a dataset of 1,248 chest X-ray images of posterior–anterior view (666 images) and anterior–posterior view (582 images) from two public repositories (Cohen et al. 2020, RSNA Pneumonia Detection Challenge (Kaggle)). The first repository contains chest X-ray images of 215 COVID-19 patients and 33 non-COVID pneumonia patients. The second repository contains chest X-ray images of 500 healthy subjects and 500 non-COVID pneumonia patients. We carefully eliminated the X-ray images of lateral view and CT images from the data cohort of first repository.

Results

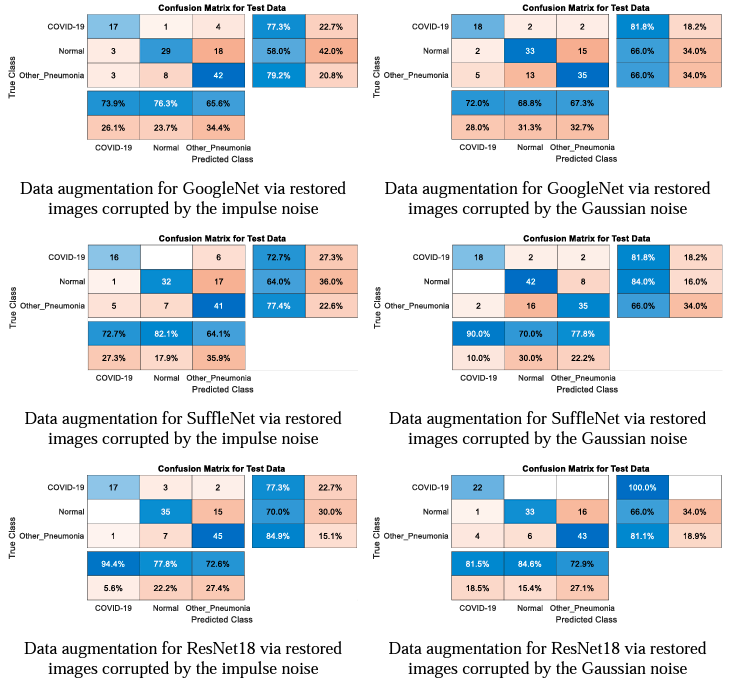
The confusion matrices of COVID-19 classification by the proposed data augmentation approach using restored images are shown in Fig. 3.

For Details

Please read our papers [1], [2].